こんにちは。構造計画研究所の山崎です。
標本調査では、どの程度の標本誤差が見込まれるかを踏まえて、サンプルサイズを決める必要があります。
そこで今回は、視聴率調査を例にとって、標本調査のサンプルサイズについて考えてみましょう。
●標本誤差の計算式
標本調査において、標本誤差は95%以下の確率で下式の値以下になります。
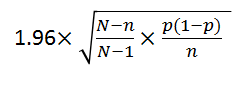
上式において、Nは母集団の大きさ、nはサンプルサイズ、pは今回の場合、全数調査した場合の視聴率です。
pに対しては予測値を用いることになりますが、予測が難しい場合、標本誤差が最も大きくなる50%を想定すれば、サンプルサイズを安全に見積もることができます。
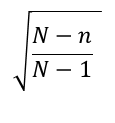の項は、母集団がサンプルサイズに対して十分大きい場合は1とみなせます。（以下ではこの項を1とみなします）
●±10%以下の誤差で結果を得たい場合、どの程度のサンプルサイズが必要？
では、p=0.5として、標本誤差を0.1以下、つまり±10%以下の誤差で結果を得たい場合、必要なサンプルサイズはいくらになるでしょうか。
これらの値を標本誤差の式に代入すると、n=96と求まります。
つまり、±10%以下の誤差で結果を得たい場合、必要なサンプルサイズは96ということがわかります。
このようにして、求めたい精度に対して適切なサンプルサイズを計算することができました。
●600世帯に対する視聴率調査の標本誤差はどの程度？
では、実際に実施されている視聴率調査は、どの程度の精度で実施されているのでしょうか。
視聴率調査で有名なビデオリサーチでは、関東地区において600世帯を対象とした調査を実施しています。
この場合、p=0.5として、n=600を代入すると、標本誤差は0.04以下（小数第三位を四捨五入）と求まります。
つまり、ビデオリサーチの関東地区の視聴率は、±4%以下の誤差を認めて算出されていることがわかります。
標本調査のサンプルサイズに関する知識は、標本調査を実施する場合にはもちろん、標本調査の調査結果を正しく理解する際にも必要です。
これを機会に、標本調査のサンプルサイズについて、一度おさらいしてみてはいかがでしょうか。
〈参考〉
・総務省統計局「標本調査とは？～調査のしくみと設計～」
・『実践アンケート調査入門』（内田治/醍醐朝美、日本経済新聞社、2001年）
